Teorema de Euclides

Para compreender a explicação de Kant acerca de como a matemática colocou-se "no caminho seguro da ciência" (Prefácio à segunda edição da Crítica da Razão Pura , Bx-xii) é necessário compreender o exemplo que ele oferece. Segundo uma nota da edição Cambridge, o teorema em pauta é o da proposição 5 do Livro I dos Elementos de Euclides. Segue a transcrição desse teorema, como encontrada aqui:

PROP. V. THEOR.

Em qualquer triangulo isosceles os angulos, que estão sobre a base, são eguaes; e produzidos os lados eguaes, os angulos, que se formam debaixo da base, são tambem eguaes ( Fig. 22 ).

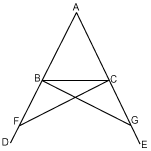Fig. 22

Seja o triangulo isosceles ABC com os lados eguaes AB, AC, os quaes sejam produzidos para D e E. Digo, que será o angulo ABC=ACB, e CBD=BCE.

Tome-se na recta BD um ponto qualquer F; e da recta AE>AF se corte ( Pr. 3, 1 ) a parte AG=AF; e se tirem as rectas FC, GB. Sendo AF=AG, e AB=AC; as duas FA, AC serão eguaes ás duas GA, AB, cada uma a cada uma. E além disto comprehendem o angulo comum FAG. Logo a base FC será egual ( Pr. 4, 1 ) á base GB; e o triangulo AFC egual ao triangulo AGB; e os mais angulos eguaes aos mesmos angulos, cada um a cada um; isto é, os que são oppostos a lados eguaes, como ACF=ABG, e AFC=AGB. E sendo AF=AG, e AB=AC, tirando AB de AF e AC de AG, ficará BF=CG ( Ax. 3 ). Mas temos demonstrado, que FC=GB. Logo as duas BF, FC são eguaes ás duas CG, GB, cada uma a cada uma; e o angulo BFC=CGB. Mas a base BC é commum aos dous triangulos FBC, GCB. Logo estes dous triangulos são eguaes ( Pr. 4, 1 ); e os mais angulos delles, que forem oppostos a lados eguaes, são tambem eguaes. Logo será o angulo FBC=GCB, e BCF=CBG. Assim sendo o angulo total ABG egual ao total ACF, como se tem demonstrado; e sendo CBG=BCF, tirando CBG de ABG e BCF de ACF, ficará o angulo ABC=ACB, que são os angulos sobre a base BC do triangulo isosceles ABC. E já se tem provado FBC=GCB, que são os angulos debaixo da base BC.

COROL. Disto se segue, que todo o triangulo equilatero é tambem equiangulo.

Newton e Leibniz sobre espaço e tempo

Olá pessoal,

Segue o link para a trradução de um ótimo texto do Lawrence Sklar: "O debate entre Newton e Leibniz " acerca do espaço e do tempo (retirado de Philosophy of Physics, de Lawrence Sklar (Oxford University Press, 1992)).

--
Um abraço,

Jonadas